Quadratic Variation and Stochastic Integration
Stochastic integration was first developed in the context of the Brownian motion and the theory was then extended to martingales with continuous paths, which we will call continuous martingales in what follows. Continuous martingales have a lot of structure which eases the corresponding stochastic integration theory. The quadratic variation of a continuous martingale is the central concept in this theory. The purpose of this note is to provide an easy introduction to this subject before presenting Ito calculus in a later post.
The quadratic variation process
The variation of order \(p\) of a trajectory \((X_{t}(\omega))_{t \in [0,T]}\) of the stochastic process \((X_{t})_{t \in [0,T]}\) for a given partition \(\pi_{[0,T]}=(t_{0}=0,t_{1},\ldots,t_{n}=T)\) of \([0,T]\) is defined as: \[V^{(p)}(\pi_{[0,T]})(\omega)=\sum_{k=1}^{n}|X_{t_{k}}(\omega)-X_{t_{k-1}}(\omega)|^{p}.\] If \(V^{(p)}(\pi_{[0,T]})(\omega)\) has a limit1 when the partitions get finer we can refer to it as \(V^{(p)}_{T}(\omega)\), the variation of order \(p\) of trajectory \(\omega\) over the time interval \([0,T]\).
For finite variation processes, we have \(V^{(1)}_{T}(\omega)<\infty\) and for \(p\>1\), it turns out that\(V^{(p)}_{T}(\omega)_{T}=0\). This is the case for instance when \((X_{t}(\omega))_{t \in [0,T]}\) is monotonic in time (increasing or decreasing) or when it can be written as the difference of two monotonic functions. Most usual functions are of this sort. In contrast, the continuous martingales have \(V^{(1)}_{T}(\omega)=+\infty\), \(V^{(2)}_{T}(\omega)<\infty\) and for \(p\>2\), \(V^{(p)}(\omega)_{T}=0\). This is easily seen in the case of the Brownian motion, the prototypical continuous martingale, as we now show.
The Brownian motion has independent non overlapping increments \(B_{t}-B_{s} \, (t \geq s)\), with law \({\cal N}(0,t-s)\). In particular, we have:\[E[(B_{t}-B_{s})^2]= t-s.\] We can thus compute the expectation of \(V^{(2)}(\pi_{[0,T]})(\omega)\): \[E[V^{(2)}(\pi_{[0,T]})(\omega)]=\sum_{k=1}^{n}|t_{k}-t_{k-1}|=T.\] We can also compute the variance of \(V^{(2)}(\pi_{[0,T]})(\omega)\): \[Var[V^{(2)}(\pi_{[0,T]})(\omega)]=E\left[\left(\sum_{k=1}^{n}|B_{t_{k}}(\omega)-B_{t_{k-1}}(\omega)|^{2}-(t_{k}-t_{k-1})\right)^{2}\right],\] where the mean of the overall variation has been re-affected to the increments. Terms within the parenthesis are independent (the Brownian increments are independent) and centered. When developing the square, the cross products thus have expectation zero and we are left with :\[Var[V^{(2)}(\pi_{[0,T]})(\omega)]=\sum_{k=1}^{n}E\left[|B_{t_{k}}(\omega)-B_{t_{k-1}}(\omega)|^{2}-(t_{k}-t_{k-1})\right]^{2}\]\[=\sum_{k=1}^{n}(t_{k}-t_{k-1})^{2}E\left[(Z_{k}^{2}-1)^{2}\right],\]where each \(Z_{k}\) is has a standard normal distribution so that \(E\left[(Z_{k}^{2}-1)^{2}\right]=1\) (cf. the properties of the chi-square distribution). We are thus left with:\[Var[V^{(2)}(\pi_{[0,T]})(\omega)]=\sum_{k=1}^{n}(t_{k}-t_{k-1})^{2}\leq T\max_{k}|t_{k}-t_{k-1}|.\]The variance of the quadratic variation thus converges to zero as the grid gets finer. This means that the quadratic variation of the Brownian motion over \([0,T]\) converges to \(T\) in the \(L^{2}\) sense as the grid gets finer and in that sense, we can say that the quadratic variation of the Brownian motion is not random:\[\boxed{V_{T}^{(2)}(\omega)=T.}\] This property almost characterizes the Brownian motion (cf. Levy’s characterization theorem).This is at first sight a surprising result. It illustrates the fact that randomness can disappear through some sort of law of large numbers in the limit of continuous time. As a final observation, we note that for a given trajectory, the quadratic variation of the Brownian motion is a strictly increasing function of time.
We now wish to consider the more general case of continuous martingales and study their quadratic variation. Some elementary algebra reveals that: \[X_{t_{i}}^{2}-X_{t_{i-1}}^{2}=2X_{t_{i-1}}(X_{t_{i}}-X_{t_{i-1}})+(X_{t_{i}}-X_{t_{i-1}})^{2}.\] Cumulating this relationship along a grid \(\pi_{[0,T]}\), we get (\(k \le n\)): \[X_{t_{k}}^{2}-X_{0}^{2}=\sum_{i=1}^2X_{t_{i-1}}(X_{t_{i}}-X_{t_{i-1}})+\sum_{i=1}^{k}(X_{t_{i}}-X_{t_{i-1}})^{2}.\] For a continuous martingale \((X_{t})_{t \in [0,T]}\), one can show that as the grid gets finer, the first term on the right hand side converges2 to a continuous martingale \((M_{t})_{t \in [0,T]}\), allowing to define a continuous process \((A_{t})_{t \in [0,T]}\) through \(A_{t}=X_{t}^{2}-X_{0}^{2}-M_{t}\) as the quadratic variation \(V^{(2)}([0,t])\). This process is increasing and as such, it is of bounded variation. It is usually noted \(([X]_{t})_{t \in [0,T]}\). Implicit in the notation \([X]_{t}\) is the initialization at \(0\).
The decomposition: \[\boxed{X_{t}^{2}-X_{0}^{2}=M_{t}+[X]_{t},}\] is called the Doob-Meyer decomposition of the submartingale \(X_{t}^{2}-X_{0}^{2}\) (see this other post). We noted that \(([X]_{t})_{t \in [0,T]}\) is increasing. One can in addition show that a continuous martingale having a constant quadratic variation process is constant. If we rule out processes that are constant on some interval of time, we therefore get continuous martingales with strictly increasing quadratic variation. The main difference with the Brownian motion is that in the latter case, quadratic variation is the deterministic function \(t\), whereas in the case of (‘nowhere constant’) continuous martingales, quadratic variation is strictly increasing but potentially random. One can actually prove that such a continuous martingale is just a time-changed Brownian motion, where the time change works like a random clock which never goes backwards. Defining the time change through: \[\tau(t)=\inf\{u:[X]_{u}\>t\},\] assuming this has a solution almost everywhere over an open interval \([0,h]\), i.e. almost everywhere \(h<[X]_{T}\). The time changed process \((B_{t}=X_{\tau(t)})_{t \in [0,h]}\) has quadratic variation \([B_{t}]=t\) and one can show that it is a Brownian motion for the time changed filtration. In other words, continuous martingales are never far from the Brownian motion (see the end of the post for another way to recover a Brownian motion from a continuous local martingale).
Stochastic Integration and the Ito Isometry
As explained in this other post, we could apply standard integration theory to make sense of expressions like \(\int_{0}^{T} H_{u}dX_{u}\) provided the process \((X_{t})_{t \in [0,T]}\) had trajectories of bounded first order variation. But this cannot be the case of a process of finite quadratic variation. Stochastic integration is therefore special. To make sense of an expression like: \[\int_{0}^{T} H_{u}dX_{u},\] the strategy consists in defining an approximation scheme whereby suitable processes \((H_{t})_{t \in [0,T]}\) get approximated by simpler processes \((H^{n}_{t})_{t \in [0,T]}\) for which \(\int_{0}^{T} H^{n}_{u}dX_{u}\) is easily defined. The trick then is to ensure that \(\int_{0}^{T} H^{n}_{u}dX_{u}\) converges in some well defined sense as \((H^{n}_{t})_{t \in [0,T]}\) converges to \((H_{t})_{t \in [0,T]}\). The key to this approximating scheme is the existence of the quadratic variation of \((X_{t})_{t \in [0,T]}\) (see the figure below).
To get a glimpse into this scheme, let’s assume \(H\) is a simple weighting scheme as defined in this other post. For such a weighting scheme, the stochastic integral is defined as: \[\int_{0}^{t}H_{u}dX_{u}=\sum_{i=0}^{J(t)-1}H^{i}(X_{T_{i+1}}-X_{T_{i}})+H^{J(t)}(X_{t}-X_{T_{J(t)}}),\] where \(J(t)(\omega)\) is set such that \(T_{J(t)}(\omega) \leq t < T_{J(t)+1}(\omega)\). We can now compute the square of the \(L^{2}\) norm of this random variable: \[E\left[\left(\int_{0}^{t}H_{u}dX_{u}\right)^{2}\right]=\] \[E\left[\left(\sum_{i=0}^{J(t)-1}H^{i}(X_{T_{i+1}}-X_{T_{i}})+H^{J(t)}(X_{t}-X_{T_{J(t)}})\right)^{2}\right].\] The martingale property implies that in the development of the squared sum, all cross products have expectation \(0\). One then gets as a result the expression: \[\sum_{i=0}^{J(t)-1}E\left[(H^{i}(X_{T_{i+1}}-X_{T_{i}}))^{2}\right]+E\left[(H^{J(t)}(X_{t}-X_{T_{J(t)}}))^{2}\right].\] For one term we have: \[E\left[(H^{i}(X_{T_{i+1}}-X_{T_{i}}))^{2}\right]=E\left[(H^{i})^{2}E_{T_{i}}\left[(X_{T_{i+1}}-X_{T_{i}})^{2}\right]\right],\] but \[E_{T_{i}}\left[(X_{T_{i+1}}-X_{T_{i}})^{2}\right]=E_{T_{i}}\left[X_{T_{i+1}}^{2}\right]-2E_{T_{i}}\left[X_{T_{i+1}}X_{T_{i}}\right]+E_{T_{i}}\left[X_{T_{i}}^{2}\right]\] \[=E_{T_{i}}\left[X_{T_{i+1}}^{2}-X_{T_{i}}^{2}\right]\] \[=E_{T_{i}}\left[[X]_{T_{i+1}}^{2}-[X]_{T_{i}}^{2}\right].\] Using these building blocks, we get: \[E\left[\left(\int_{0}^{t}H_{u}dX_{u}\right)^{2}\right]=\] \[E\left[\sum_{i=0}^{J(t)-1}(H^{i})^{2}([X]_{T_{i+1}}-[X]_{T_{i}})+(H^{J(t)})^{2}([X]_{t}-[X]_{T_{J(t)}})\right],\] but this last term is the ‘usual’ integral of \(H\) against the increasing process \([X]\). We can thus write:\[E\left[\left(\int_{0}^{t}H_{u}dX_{u}\right)^{2}\right]=E\left[\int_{0}^{t}H_{u}^{2}d[X]_{u}\right].\]
This result, recast as: \[\boxed{\left(E\left[\left(\int_{0}^{T}H_{u}dX_{u}\right)^{2}\right]\right)^{1/2}=\left(E\left[\int_{0}^{T}H_{u}^{2}d[X]_{u}\right]\right)^{1/2}.}\] is called the Ito isometry property of stochastic integrals. It essentially shows that stochastic integration as a mapping from the simple weight function \((H_{t})_{t \in [0,T]}\) to \(\int_{0}^{T}H_{u}dX_{u}\) preserves a notion of norm, where the norm of \((H_{t})_{t \in [0,T]}\) is defined as \[\|H\|_{[X]}=\left(E\left[\int_{0}^{T}H_{u}^{2}d[X]_{u}\right]\right)^{1/2}\] while the norm of the random variable \(\int_{0}^{T}H_{u}dX_{u}\) is defined as \[\|\int HdX\|=\left(E\left[\left(\int_{0}^{T}H_{u}dX_{u}\right)^{2}\right]\right)^{1/2}.\] Both spaces are so called \(L^{2}\) spaces.
Using this isometry property, one can extend the stochastic integral beyond simple weights to ‘progressively measurable3 weights’ with finite norm. The nature of the norm on weight functions involves the quadratic variation function of the continuous martingale. It is thus not surprising to see that what counts in the most general formulation of stochastic integration versus continuous martingale is the finiteness for all \(t\) and almost all events \(\omega\) of: \[\int_{0}^{t}H_{u}^{2}d[X]_{u}.\] This is, together with progressive measurability, the key condition for stochastic integration to be meaningful.
The overall situation is summarized in the following figure: 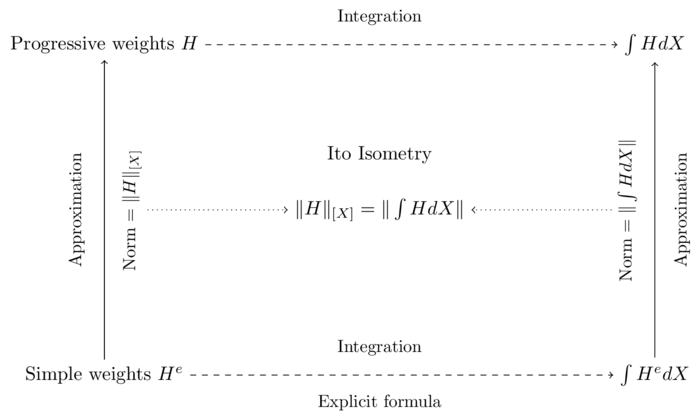
The Quadratic Variation of a Stochastic Integral
The reader who has made it so far will not be surprised by the following result: \[[\int_{0}^{\cdot}H_{u}dX_{u}]_{t}=\int_{0}^{t}(H_{u})^{2}d[X]_{u},\] which is easily guessed from the basic definition of the stochastic integral for simple weights. We can extend this result to covariation, which we now define.
We are given two continuous martingales \((X_{t})_{t \in [0,T]}\) and \((Y_{t})_{t \in [0,T]}\). We can study their covariation \[Cov(\pi_{[0,T]})(\omega)=\sum_{k=1}^{n}(X_{t_{k}}(\omega)-X_{t_{k-1}}(\omega))(Y_{t_{k}}(\omega)-Y_{t_{k-1}}(\omega)).\] Fortunately, we do not need to work too hard now. Indeed, we can simply use the so-called polarization identity: \[ab=\frac{1}{4}\left((a+b)^{2}-(a-b)^{2}\right),\] to directly define covariation from variation:\[[X,Y]_{t}=\frac{1}{4}\left([X+Y]_{t}-[X-Y]_{t}\right).\] With this notation, \([X]\) is the covariation of \(X\) with itself \([X,X]\). Finally, just as \(([X]_{t})_{t \in [0,T]}\) is characterized by the fact that \((X_{t}-[X]_{t})_{t \in [0,T]}\) is a martingale, \(([X,Y]_{t})_{t \in [0,T]}\) is characterized by the fact that \((X_{t}Y_{t}-[X,Y]_{t})_{t \in [0,T]}\) is a martingale.
We now have:\[\boxed{[\int_{0}^{\cdot}H_{u}dX_{u},\int_{0}^{\cdot}G_{u}dY_{u}]_{t}=\int_{0}^{t}H_{u}G_{u}d[X,Y]_{u},}\] for the covariation of two stochastic integrals with respect to two continuous integrals.
To end this post, let’s assume we can define for a given martingale \((X_{t})_{t \in [0,T]}\) a process \((H_{t})_{t \in [0,T]}\) through: \[\int_{0}^{t}(H_{u})^{2}d[X]_{u}=t.\] Then, by construction, the process \(Y_{t}=\int_{0}^{t}H_{u}dX_{u}\) has quadratic covariation \([Y]_{t}=t\). One can show that \((Y_{t})_{t \in [0,T]}\) is a Brownian motion. This construction is possible if \(([X]_{t})_{t \in [0,T]}\) can be written: \[[X]_{t}=\int_{0}^{t}v_{u}du\] with \(v_{u}\) almost everywhere strictly positive. One can then indeed pick \(H_{u}=1/(v_{u})^{1/2}\). The Brownian motion is hidden, but it is never very far.
Links
See Karatzas Shreve (1991), Brownian Motion and Stochastic Calculus, Springer, pp 32-35.↩︎
Convergence takes place in probability uniformly with respect to time on compact time intervals.↩︎
In stochastic integration theory, we need variables to be adapted to the underlying filtration. This allows to make sense of the notion of information which is key to the interpretation of the calculus. We need also time averages and time integrals to lead to well-defined random variables. This means that, as a function of time and outcome \(\omega\), a process \(X(\cdot,\cdot)\) should be measurable with respect to the product sigma algebra jointly generated by the Borel sets on the time axis and the probabilistic filtration on the \(\omega\) axis.↩︎